设A B都是n级实对称矩阵 并且AB=B A．证明：存在一个n级正交矩阵T 使得TAT与TBT都为对

正确答案：因为A是咒级实对称陈所以存在正交矩阵T₁使得T₁^-1AT₁=diag(λ₁I_r1λ₂I_r2…λ_mI_rm)其中λ₁λ₂…λ_m是A的全部不同的特征值．由已知条件AB—BA得AT₁T₁^-1B=BT₁T₁^-1A则(T₁^-1AT₁)(T₁^-1BT₁)=(T₁^-1BT₁)(T₁^-1AT₁)即diag(λ₁I_r1λ₂I_r2…λ_mI_rm)从而(T₁^-1BT₁)=diag(B₁B₂…B_n)其中每个B_i为实对称矩阵．因为B_i为实对称矩阵故存在正交矩阵P_i使P_i^'B_iP_i为对角矩阵令P=diag(P₁P₂…P_m)则P为一正交矩阵T=T₁P为正交矩阵且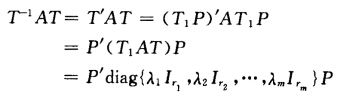则可知T^-1AT为一对角矩阵．而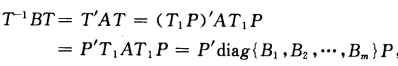这可知T^-1BT为一对角阵故命题成立．
因为A是咒级实对称陈,所以存在正交矩阵T1,使得T1-1AT1=diag(λ1Ir1,λ2Ir2,…,λmIrm)其中λ1,λ2,…,λm是A的全部不同的特征值．由已知条件AB—BA,得AT1T1-1B=BT1T1-1A,则(T1-1AT1)(T1-1BT1)=(T1-1BT1)(T1-1AT1)即diag(λ1Ir1,λ2Ir2,…,λmIrm),从而(T1-1BT1)=diag(B1,B2,…,Bn),其中每个Bi为实对称矩阵．因为Bi为实对称矩阵,故存在正交矩阵Pi使Pi'BiPi为对角矩阵,令P=diag(P1,P2,…,Pm),则P为一正交矩阵,T=T1P为正交矩阵且则可知T-1AT为一对角矩阵．而这可知T-1BT为一对角阵,故命题成立．