用Gerschgorin圆盘定理证明:矩阵能够相似于对角矩阵且A的特征值都是正实数.请帮忙给出正确答
用Gerschgorin圆盘定理证明:矩阵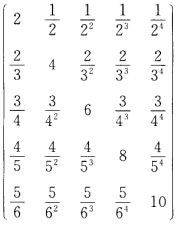 能够相似于对角矩阵且A的特征值都是正实数.
能够相似于对角矩阵且A的特征值都是正实数.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:A的5个盖尔网盘为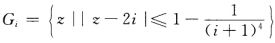 i=12345它们都是孤立的从而矩阵有5个互异特征值所以矩阵能够相似于对角矩阵再由Gi关于实轴对称且都在y坐标轴右边以及实矩阵的复数特征值成对共扼出现的性质知Gi中的特征值必为正实数所以A的特征值都是正实数.
i=12345它们都是孤立的从而矩阵有5个互异特征值所以矩阵能够相似于对角矩阵再由Gi关于实轴对称且都在y坐标轴右边以及实矩阵的复数特征值成对共扼出现的性质知Gi中的特征值必为正实数所以A的特征值都是正实数.
A的5个盖尔网盘为,i=1,2,3,4,5,它们都是孤立的,从而矩阵有5个互异特征值,所以矩阵能够相似于对角矩阵,再由Gi关于实轴对称且都在y坐标轴右边,以及实矩阵的复数特征值成对共扼出现的性质知,Gi中的特征值必为正实数,所以A的特征值都是正实数.
相似问题
证明:如果一个实对称矩阵A的主对角元都大于零 则A至少有一个正的特征值.请帮忙给出正确答案和分析 谢
证明:如果一个实对称矩阵A的主对角元都大于零,则A至少有一个正的特征值.请帮忙给出正确答案和分析,谢谢!
设x为n×m矩阵 A B分别为n×n和m×n的常数矩阵 证明: 请帮忙给出正确答案和分析 谢谢!
设x为n×m矩阵,A,B分别为n×n和m×n的常数矩阵,证明: 请帮忙给出正确答案和分析,谢谢!
设A=(αij)∈Cn×n 满足 (i=1 2 … n) 则 (1)A可逆; (2)请帮忙给出正确答
设A=(αij)∈Cn×n,满足 (i=1,2,…,n),则 (1)A可逆; (2)请帮忙给出正确答案和分析,谢谢!
设f(x)=tr(XTX) x∈Rm×n 求请帮忙给出正确答案和分析 谢谢!
设f(x)=tr(XTX),x∈Rm×n,求请帮忙给出正确答案和分析,谢谢!
设A为正定Hermite矩阵 B为反Hermite矩阵.试证明:AB与BA的特征值实部为零. (2)
设A为正定Hermite矩阵,B为反Hermite矩阵.试证明:AB与BA的特征值实部为零. (2)设A是n(n>1)阶正定矩阵.α是非零列向量,且α∈Rn.令B=AααT,求B的












