在以下情况下 平行板电容器的电容 内部的电场强度 储存的电场能及两极板的电势差和电荷将如何变化？（1

正确答案：（1）断开电源则极板的电量无变化即Q=Q₀ （1）电容器的电容取决于其几何参量和其中电介质的电容率由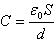可知电容变为 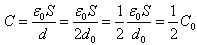（2）因为σ=Q/S=Q₀/S所以电场强度为 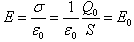（3）储存的电场能为 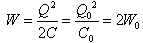（4）两极板的电势差为△U=Ed=E₀.2d₀=2△U₀ （5）（2）断开电源则极板的电量无变化即Q=Q₀ （6）电容器的电容取决于其几何参量和其中电介质的电容率由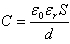可知电容变为 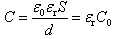（7）因为σ=Q/S=Q₀/S所以电场强度为 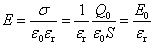（8）储存的电场能为 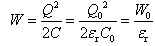（9）两极板的电势差为 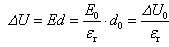（10）（3）保持电源连接状态则极板间的电势差无变化即△U=△U₀ （11）电容器的电容取决于其几何参量和其中电介质的电容率由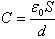可知电容变为 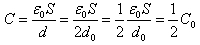（12）因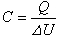为所以电量为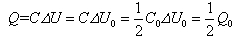 （13）因为σ=Q/S=Q₀/S所以电场强度为 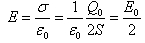（14）储存的电场能为 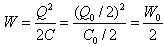（15）（4）保持电源连接状态则极板间的电势差无变化即△U=△U₀ （16）电容器的电容取决于其几何参量和其中电介质的电容率由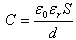可知电容变为 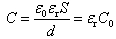（17）因为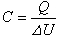所以电量为Q=C△U=C△U₀=ε_rC₀△U₀=ε_rQ₀（18）因为 所以电场强度为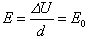（19）储存的电场能为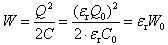
（1）断开电源,则极板的电量无变化,即Q=Q0（1）电容器的电容取决于其几何参量和其中电介质的电容率,由可知,电容变为（2）因为σ=Q/S=Q0/S,所以电场强度为（3）储存的电场能为（4）两极板的电势差为△U=Ed=E0.2d0=2△U0（5）（2）断开电源,则极板的电量无变化,即Q=Q0（6）电容器的电容取决于其几何参量和其中电介质的电容率,由可知,电容变为（7）因为σ=Q/S=Q0/S,所以电场强度为（8）储存的电场能为（9）两极板的电势差为（10）（3）保持电源连接状态,则极板间的电势差无变化,即△U=△U0（11）电容器的电容取决于其几何参量和其中电介质的电容率,由可知,电容变为（12）因为,所以电量为（13）因为σ=Q/S=Q0/S,所以电场强度为（14）储存的电场能为（15）（4）保持电源连接状态,则极板间的电势差无变化,即△U=△U0（16）电容器的电容取决于其几何参量和其中电介质的电容率,由可知,电容变为（17）因为,所以电量为Q=C△U=C△U0=εrC0△U0=εrQ0（18）因为,所以电场强度为（19）储存的电场能为