老王每月收入120元。全部用来购买商品X和Y。他的效用函数为U=XY X的价格是2元。Y的价格是3元
老王每月收入120元。全部用来购买商品X和Y。他的效用函数为U=XY,X的价格是2元。Y的价格是3元。试求：
为使老王的效用最大化，他购买的X和Y各为多少?
请帮忙给出正确答案和分析，谢谢！
参考解答
427***774
2024-06-11 06:35:54
正确答案：预算线方程为2X+3Y=120。构造拉格朗日辅助函数L=XY一λ(2X+3Y一120)。拉格朗日定理认为最优选择必定满足以下三个一阶条件：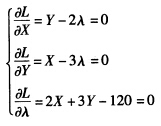
解得：X=30Y=20。即为使老王的效用最大化他应购买30单位X商品20单位Y商品。
预算线方程为2X+3Y=120。构造拉格朗日辅助函数L=XY一λ(2X+3Y一120)。拉格朗日定理认为,最优选择必定满足以下三个一阶条件：解得：X=30,Y=20。即为使老王的效用最大化,他应购买30单位X商品,20单位Y商品。
相似问题
给定一个理性的消费者效用函数为U(X1 X2)= 商品价格分别为P1=2 P2=1 如果该消费者选择
给定一个理性的消费者效用函数为U(X1，X2)=，商品价格分别为P1=2、P2=1，如果该消费者选择了X1=4，那么该消费者可用于两种商品支出的预算收入是多少?( )
假定政府规定烟叶的最低收购价格w=12 且禁止低于最低收购价的交易行为 则烟叶种植农户与香烟生产者的
假定政府规定烟叶的最低收购价格w=12，且禁止低于最低收购价的交易行为，则烟叶种植农户与香烟生产者的剩余变化如何?(上海财经大学2005研)请帮忙给出正确
如果Py=14。此人将消费多少x?(上海交通大学2005研)请帮忙给出正确答案和分析 谢谢！
如果Py=14。此人将消费多少x?(上海交通大学2005研)请帮忙给出正确答案和分析，谢谢！
棉花市场需求函数为Qd=10一2p1。供给函数为Qs=3p一5 政府为了保护棉农利益 决定采取适当政
棉花市场需求函数为Qd=10一2p1。供给函数为Qs=3p一5，政府为了保护棉农利益，决定采取适当政策。政府决定制定最低价格，并决定按照最低p=4收购市场上剩余
某人消费X和Y 他的效用函数为U=min{x+2y 4x+y}。如果X和Y的价格分别为4和5 那么他
某人消费X和Y，他的效用函数为U=min{x+2y，4x+y}。如果X和Y的价格分别为4和5，那么他至少要花多少钱，才能使其效用水平与消费4单位X和3单元Y时一样?( )(
