1-1-6如图(a)所示 一平行光束投射在狭缝S1和S2上 两条缝与互相正交的两屏的交线的距离均为α
1-1-6如图(a)所示,一平行光束投射在狭缝S1和S2上,两条缝与互相正交的两屏的交线的距离均为α,光束的投射方向与两屏的夹角均为45°。若在距缝S1的屏为b之处,有一与这屏平行的接收屏,且b>>α。 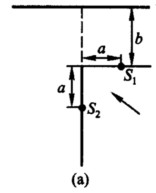 若将S1与S2视为线光源,且认为光源为单色光。 (1)试求相长和相消的条件; (2)证明在零级附近,相邻相长和相消干涉条纹间的距离不变,且为(k/2α)λ,式中 k2=(α+b)2+b2
若将S1与S2视为线光源,且认为光源为单色光。 (1)试求相长和相消的条件; (2)证明在零级附近,相邻相长和相消干涉条纹间的距离不变,且为(k/2α)λ,式中 k2=(α+b)2+b2
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:解: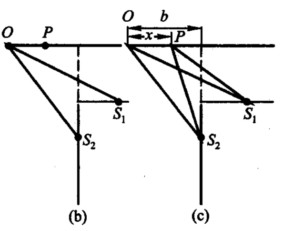 (1)如图(b)所示在接收屏上O点光程差 S2O-S1O=0将产生相长干涉.相长干涉的条件为 S2P-S1P=jλ j=0±1±2…式中P为接收屏上位于S2左边的点在S2的右侧不会形成干涉条纹相消干涉的条件为 S2P-S1P=(2j+1)λ/2 j=0±1±2…(2)如图(c)所示计算离开0级干涉的距离x S2P=[(α+b)2+(b-x)21/2 S1P=[b2+(α+b-x)21/2 S2P-S1P=[(α+b)2+(b-x)21/2-[b2+(α+b-x)21/2=jλ j=0±1±2… (x<b相长干涉) S2P-S1P=(2j+1)λ/2 j=0±l±2… (x<b相消干涉)若x=0则 S2P=S1P=[(α+b)2+b21/2且j=0相长干涉考察接收屏上的0级附近(即O附近)区域x很小时应用牛顿二项式得
(1)如图(b)所示在接收屏上O点光程差 S2O-S1O=0将产生相长干涉.相长干涉的条件为 S2P-S1P=jλ j=0±1±2…式中P为接收屏上位于S2左边的点在S2的右侧不会形成干涉条纹相消干涉的条件为 S2P-S1P=(2j+1)λ/2 j=0±1±2…(2)如图(c)所示计算离开0级干涉的距离x S2P=[(α+b)2+(b-x)21/2 S1P=[b2+(α+b-x)21/2 S2P-S1P=[(α+b)2+(b-x)21/2-[b2+(α+b-x)21/2=jλ j=0±1±2… (x<b相长干涉) S2P-S1P=(2j+1)λ/2 j=0±l±2… (x<b相消干涉)若x=0则 S2P=S1P=[(α+b)2+b21/2且j=0相长干涉考察接收屏上的0级附近(即O附近)区域x很小时应用牛顿二项式得
解:(1)如图(b)所示,在接收屏上O点,光程差S2O-S1O=0将产生相长干涉.相长干涉的条件为S2P-S1P=jλ,j=0,±1,±2,…式中,P为接收屏上位于S2左边的点,在S2的右侧不会形成干涉条纹,相消干涉的条件为S2P-S1P=(2j+1)λ/2,j=0,±1,±2,…(2)如图(c)所示,计算离开0级干涉的距离x,S2P=[(α+b)2+(b-x)21/2S1P=[b2+(α+b-x)21/2S2P-S1P=[(α+b)2+(b-x)21/2-[b2+(α+b-x)21/2=jλ,j=0,±1,±2,…(x<b,相长干涉)S2P-S1P=(2j+1)λ/2,j=0,±l,±2,…(x<b,相消干涉)若x=0,则S2P=S1P=[(α+b)2+b21/2且j=0,相长干涉考察接收屏上的0级附近(即O附近)区域,x很小时,应用牛顿二项式,得
相似问题
当一束光波入射到两种介质的均匀分界面上时 一般会产生( )现象;当满足( )的条件时 会出现全反射现
当一束光波入射到两种介质的均匀分界面上时,一般会产生( )现象;当满足( )的条件时,会出现全反射现象;当满足( )的条件时,会出现“全透射”现象。
如图8—8a所示干涉装置 点光源S位于透镜的物方焦点上 P为半透明观察屏 A为平面反射镜 P和A的夹
如图8—8a所示干涉装置,点光源S位于透镜的物方焦点上,P为半透明观察屏,A为平面反射镜,P和A的夹角δ很小。试解释该装置的工作原理、观察屏上的条纹形
两束光波的波动方程分别为y1=Acos(ωt+φ1)和y2=Acos(ωt+φ2) 两波叠加将产生干
两束光波的波动方程分别为y1=Acos(ωt+φ1)和y2=Acos(ωt+φ2),两波叠加将产生干涉现象,它们合成波的振幅为( )。请帮忙给出正确答案和分析,谢谢!
在楔形平板的双光束干涉中 A.楔角越小 条纹间隔越宽。B.楔角一定时 照射波长越长 条纹问隔越宽。C
在楔形平板的双光束干涉中,A.楔角越小,条纹间隔越宽。B.楔角一定时,照射波长越长,条纹问隔越宽。C.局部高度变化越大,条纹变形越严重。D.将该楔
设一个平面透射光栅的缝宽为α 缝间隔为d 以波长为λ的光垂直入射。若它的缝数N增大 则A.光栅的分辨
设一个平面透射光栅的缝宽为α,缝间隔为d,以波长为λ的光垂直入射。若它的缝数N增大,则A.光栅的分辨本领提高。B.光栅衍射图样中的亮纹变细。C.两亮












