试证：对于每一个实对称矩阵A 都存在一个n阶方阵S 使A=S3．请帮忙给出正确答案和分析 谢谢！
试证：对于每一个实对称矩阵A，都存在一个n阶方阵S，使A=S3．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-12 00:27:18
正确答案：矩阵A是一个对称矩阵则A酉相似于一个对角矩阵即A=Udiag(λ1λ2…λn)UH．令D=diag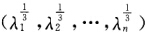
则D3=diag(λ1λ2…λn)．又由A=UD3UH=(UDUH)(UDUH)(UDUH)令S=UDUH则A=S3．
矩阵A是一个对称矩阵,则A酉相似于一个对角矩阵,即A=Udiag(λ1,λ2,…,λn)UH．令D=diag,则D3=diag(λ1,λ2,…,λn)．又由A=UD3UH=(UDUH)(UDUH)(UDUH),令S=UDUH,则A=S3．
相似问题
设A∈Cm×m和B∈Cn×n均可逆 证明： (1)若D∈Cm×n是左可逆的 则ADB是左可逆的； (
设A∈Cm×m和B∈Cn×n均可逆，证明： (1)若D∈Cm×n是左可逆的，则ADB是左可逆的； (2)若D∈Cm×n是右可逆的，则ADB是右可逆的．请帮忙给出正确答案和分析，谢谢！
设P是酉矩阵 A=diag(a1 a2 … an) 证明PA的特征值μ满足不等式m≤∣μ∣≤M 其中
设P是酉矩阵，A=diag(a1，a2，…，an)，证明PA的特征值μ满足不等式m≤∣μ∣≤M，其中m=min∣ai∣，M=max∣ai∣．请帮忙给出正确答案和分析，谢谢！
证明：(A+)+=A．请帮忙给出正确答案和分析 谢谢！
证明：(A+)+=A．请帮忙给出正确答案和分析，谢谢！
讨论下列幂级数的敛散性： (1)； (2)请帮忙给出正确答案和分析 谢谢！
讨论下列幂级数的敛散性： (1)； (2)请帮忙给出正确答案和分析，谢谢！
设A B∈Cn×n AB=BA 证明： sin(A+B)=sin Acos B+cos Asin B
设A，B∈Cn×n，AB=BA，证明： sin(A+B)=sin Acos B+cos Asin B，cos(A+B)=cos Acos B－sin Asin B．请帮忙给出正确答案和分析，谢谢！
