分块对角矩阵A—diag{A1 A2 … As)可逆的充分必要条件是它的主对角线上每个子矩阵Ai可逆
分块对角矩阵A—diag{A1，A2，…，As)可逆的充分必要条件是它的主对角线上每个子矩阵Ai可逆，并且当A可逆时，有A-1=diag{A1-1，A2-1，…，As-1}．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***101
2024-11-14 00:45:49
正确答案：如果A可逆则｜A｜≠0即｜A1｜.｜A2｜…｜As｜≠0所以｜Ai｜≠0 i=12…s所以A1A2…As均可逆反之如果每个子矩阵Ai可逆则｜Ai｜≠0故｜A｜=｜A1｜｜A2｜…｜As｜≠0所以A可逆diag{A1A2…As).diag{A1-1A2-1…As-1)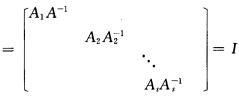
所以A-1=diag{A1-1A2-1…A3-1
如果A可逆,则｜A｜≠0即｜A1｜.｜A2｜…｜As｜≠0,所以｜Ai｜≠0i=1,2,…,s所以A1,A2,…,As均可逆反之如果每个子矩阵Ai可逆,则｜Ai｜≠0,故｜A｜=｜A1｜｜A2｜…｜As｜≠0,所以A可逆diag{A1A2…As).diag{A1-1A2-1…As-1)所以A-1=diag{A1-1,A2-1…A3-1
相似问题
设A B分别是数域K上s×n n×s矩阵 证明：AB与BA有相同的非零特征值．请帮忙给出正确答案和分
设A、B分别是数域K上s×n，n×s矩阵，证明：AB与BA有相同的非零特征值．请帮忙给出正确答案和分析，谢谢！
设A B分别是s×n n×s矩阵 证明：请帮忙给出正确答案和分析 谢谢！
设A，B分别是s×n，n×s矩阵，证明：请帮忙给出正确答案和分析，谢谢！
如果向量组α1 α2 α3线性无关 则向量组2α1+α2 α2+5α3 4α3+3α1也线性无关．请
如果向量组α1,α2,α3线性无关，则向量组2α1+α2，α2+5α3，4α3+3α1也线性无关．请帮忙给出正确答案和分析，谢谢！
设A=diag{α1In1 α2In2 … αsIns) 其中α1 α2 … αs是两两不同的数．证
设A=diag{α1In1，α2In2，…，αsIns)，其中α1，α2，…，αs是两两不同的数．证明：与A可交换的矩阵一定是分块对角矩阵ding{B2，B2，…，Bs}，其中Bi
设A是实数域上的s×n矩阵 β是R2的任意一个列向量．证明：n元线性方程组AAX=Aβ一定有解．请帮
设A是实数域上的s×n矩阵，β是R2的任意一个列向量．证明：n元线性方程组AAX=Aβ一定有解．请帮忙给出正确答案和分析，谢谢！
