设A=(αij)∈Cn×n 满足 (i=1 2 … n) 则 (1)A可逆； (2)请帮忙给出正确答
设A=(αij)∈Cn×n，满足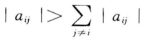
(i=1，2，…，n)，则 (1)A可逆； (2)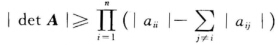
请帮忙给出正确答案和分析，谢谢！
参考解答
406***101
2024-11-12 00:48:48
正确答案：(1)因为A为严格对角占优矩阵由定理4知A可逆． (2)设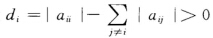
令
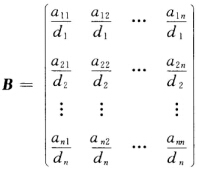则有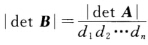
所以B盖尔圆盘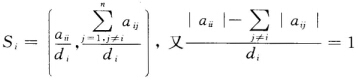
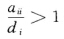并且Si与单位圆相外切故矩阵B的特征值的模均大于1所以∣det B∣≥1即
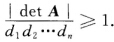所以
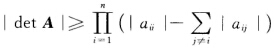成立．
(1)因为A为严格对角占优矩阵,由定理4知,A可逆．(2)设,令,则有,所以B盖尔圆盘,并且Si与单位圆相外切,故矩阵B的特征值的模均大于1,所以∣detB∣≥1,即,所以成立．
相似问题
设f(x)=tr(XTX) x∈Rm×n 求请帮忙给出正确答案和分析 谢谢！
设f(x)=tr(XTX)，x∈Rm×n，求请帮忙给出正确答案和分析，谢谢！
设A为正定Hermite矩阵 B为反Hermite矩阵．试证明：AB与BA的特征值实部为零． (2)
设A为正定Hermite矩阵，B为反Hermite矩阵．试证明：AB与BA的特征值实部为零． (2)设A是n(n>1)阶正定矩阵．α是非零列向量，且α∈Rn．令B=AααT，求B的
设A B都是实对称矩阵 A的一切特征值在区间[a b]上 B的一切特征值在区间 [c d]上．证明：
设A，B都是实对称矩阵，A的一切特征值在区间[a，b]上，B的一切特征值在区间 [c，d]上．证明：A+B的特征值必在区间[a+c，b+d]上．请帮忙给出正确答案和分析，谢谢！
设PE∈Cm×m Q∈Cn×n均为可逆矩阵 且有B=PAQ 证明：Q－1A－P－1∈B{1}．请帮忙
设PE∈Cm×m，Q∈Cn×n均为可逆矩阵，且有B=PAQ，证明：Q－1A－P－1∈B{1}．请帮忙给出正确答案和分析，谢谢！
用Schmidt正交化方法求矩阵A的分解 其中请帮忙给出正确答案和分析 谢谢！
用Schmidt正交化方法求矩阵A的分解，其中请帮忙给出正确答案和分析，谢谢！
