设y=y(x) z=z(x)是由方程z=xf(x+y)和F(x y z)=0所确定的函数 其中f和F
设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数,其中f和F分别具有一阶连续导数和一阶连续偏导数,求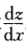 .
.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案: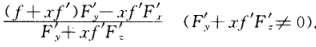 .
.
.
相似问题
设可微函数f(x y)在点(x0 y0)取得极小值 则下列结论正确的是A.f(x0 y)在y=y0处
设可微函数f(x,y)在点(x0,y0)取得极小值,则下列结论正确的是A.f(x0,y)在y=y0处的导数等于零.B.f(x0,y)在y=y0处的导数大于零.C.f(x0,y)在y=
设生产某种产品必须投入两种要素 x1和x2分别为两要素的投入量 Q为产出量;若生产函数为Q=2x1α
设生产某种产品必须投入两种要素,x1和x2分别为两要素的投入量,Q为产出量;若生产函数为Q=2x1αx2β,其中α,β为常数,且α+β=1,假设两种要素的
设平面薄片所占的闭区域D是由螺线ρ=2ψ上一段弧(0≤ψ≤π/2)与射线ψ=π/2所围成 它的面密度
设平面薄片所占的闭区域D是由螺线ρ=2ψ上一段弧(0≤ψ≤π/2)与射线ψ=π/2所围成,它的面密度为μ(x,y)=x2+y2,求这薄片的质量.请帮忙给出正确
设P(x1 y1)是椭圆外的一点 若Q(x2 y2)是椭圆上离P最近的一点 证明PQ是椭圆的法线.请
设P(x1,y1)是椭圆外的一点,若Q(x2,y2)是椭圆上离P最近的一点,证明PQ是椭圆的法线.请帮忙给出正确答案和分析,谢谢!
设f(x) g(x)是C(2)类函数 证明:函数u=f(s+at)+g(s-at)满足波动方程请帮忙
设f(x),g(x)是C(2)类函数,证明:函数u=f(s+at)+g(s-at)满足波动方程请帮忙给出正确答案和分析,谢谢!












