设A为一个n级实对称矩阵 证明：如果｜A｜

正确答案：因为｜A｜<0｜A｜≠0所以R(A)=n故存在非退化线性替换X=C^-1Y使X^TAX=Y^T(C^-1)^TACY=Y^TBY=y₁²+y₂²+…+y_p²一y_p+1²一y_p+2²一y_n²由此可知在规范形中必含有带负号的平方项故存在CX=Y即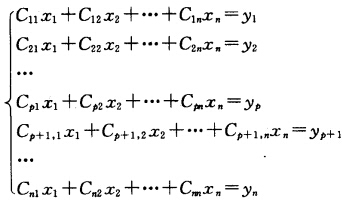令y₁=y₂=…=y_p=0y_p+1=y_p+2=…=y_n=1得线性方程组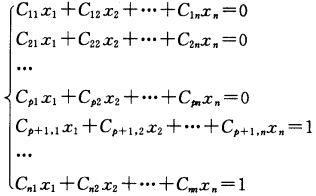又因为｜C｜≠0故方程组有唯一非零解且解为X_ε=(a₁a₂…a_n)^T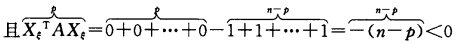即存在非零列向量α使得α^TAα<0．
因为｜A｜<0,｜A｜≠0,所以R(A)=n,故存在非退化线性替换X=C-1Y,使XTAX=YT(C-1)TACY=YTBY=y12+y22+…+yp2一yp+12一yp+22一yn2由此可知,在规范形中,必含有带负号的平方项,故存在CX=Y,即令y1=y2=…=yp=0,yp+1=yp+2=…=yn=1得线性方程组又因为｜C｜≠0,故方程组有唯一非零解,且解为Xε=(a1,a2,…,an)T即存在非零列向量α,使得αTAα<0．