如图1 二次函数y=1/2x2-2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A B两点
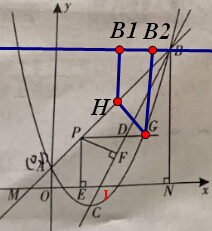
如图1，二次函数y=1/2x2-2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A，B两点，点A的坐标为（0,1），点B在第一象限内，点C是二次函数图象的顶点，点M是一次函数y=kx+b(k≠0)的图象与x轴的交点，过点B作 x轴的垂线，垂足为N，且S△AMO：S四边形AONB=1：48.
（1）求直线AB和直线BC的解析式；
（2）点P是线段AB上一点，点D是线段BC上一点，PD//x轴，射线PD与抛物线交于点G，过点P作PE⊥x轴于点E，PF⊥BC于点F，当PF与PE的乘积最大时，在线段AB上找一点H（不与点A，点B重合），使GH+ √2/2BH的值最小，求点H的坐标和GH+√2/2BH的最小值；
（3）如图2，直线AB上有一点K（3,4），将二次函数1/2x2-2x+1沿直线BC平移，平移的距离是t(t≥0)，平移后抛物线使点A，点C的对应点分别为点A’，点C’；当△A’C’K是直角三角形时，求t的值。
参考解答
406***112
2025-01-18 08:01:33
正确答案：
解：（1）C（2，-1）.
由S△AMO：S四边形AONB=1：48，可得由S△AMO：S△BMN=1：49，
所有BN=7，带入二次函数解析式可得B（6,7）。
所以yAB=x+1，yBC=2x-5.
相似问题
点P的坐标是（a b） 从-2 -1 0 1 2这五个数中任取一个数作为a的值 再从余下的四个数中任
点P的坐标是（a,b），从-2，-1,0,1,2这五个数中任取一个数作为a的值，再从余下的四个数中任取一个数作为b的值，则点P（a ,b）在平面直角坐标系中第二象
6N刚好全部浸入时读数为 9.5N。书籍首饰为某一单一材质制成 则该首饰用的材质为(g=10N/kg
6N刚好全部浸入时读数为 9 5N。书籍首饰为某一单一材质制成，则该首饰用的材质为(g=10N kg，ρ水= 1 0×103kg m3， ρ铜= 8 9×103kg m3，ρ银= 10
甲 乙两名射击运动员中进行射击比赛 两人在相同条件下各射击10次 射击的成绩如图10所示.根据图中信
甲、乙两名射击运动员中进行射击比赛，两人在相同条件下各射击10次，射击的成绩如图10所示 根据图中信息，回答下列问题：(1)甲的平均数是__，乙的中位数
如图8 在Rt△ABC中 ∠ACB=90° AC=2√3 以点C为圆心 CB的长为半径画弧 与AB边
如图8，在Rt△ABC中，∠ACB=90°，AC=2√3,以点C为圆心，CB的长为半径画弧，与AB边交于点D,将⌒BD绕点D旋转180°后点B与点A恰好重合，则图中阴影部分的面积为___
解方程：(1/x-2)-3=x-1/2-x
解方程：(1 x-2)-3=x-1 2-x
